Numpy Array对象
- ndarray是不可变对象
1. ndarray类的基本属性
- shape:元组
- size:数组中元素的总数
- ndim:维度的数量
- nbytes:存储数据的字节数
- dtype:数组中元素的数据类型
2. 数据类型
| dtype | 变体 | 说明 |
|---|---|---|
| int | intn(n = 8, 16, 32, ···) | |
| uint | uintn(n = 8, 16, 32, ···) | 无符号整型 |
| bool | Bool | |
| float | floatn | 浮点类型 |
| complex | complexN | 复数浮点型 |
- 还支持其他非数字类型:字符串、对象等
- 默认的数据类型是float
- ndarray对象创建后的dtype不能更改,除非复制数组进行类型转换:
data = np.array([1, 2, 3],dtype = np.float) # 类型转换 data = np.array(data, dtype = np.int)- 也可以使用
astype方法:
data.astype(np.int) - 也可以使用
- 在进行运算时,数据类型可能会发生转变。
- 将浮点类型与复数浮点类型——>复数类型
实部与虚部
- 不管的type的类型是什么,ndarray实例都具有real和imag属性
创建数组
| 函数名 | 数组类型 |
|---|---|
| np.arry | 使用类数组对象创建 |
| np.zeros | |
| np.ones | |
| np.fill | 创建指定数值填充的数组 |
| np.diag | |
| np.arange | 指定开始值,结束值以及增量值(不包含结束值) |
| np.linspace | 指定开始值,结束值,元素数量(包含结束值) |
| np.logspace | 等比数列,指定开始值和结束值是可选参数base的幂次(默认为10) |
| np.meshgrid | 从一维坐标向量生成坐标矩阵(或高维坐标数组) |
| np.fromfunction | |
| np.fromfile | |
| np.loadtxt | 从文本文件读取数据以创建数组 |
| np.genfromtxt | 相比于loadtxt,还支持处理缺失值 |
| np.random.rand | 0,1之间分布的随机数 |
meshgrid
将一维坐标向量转换为多维网格坐标矩阵,便于在多维空间中计算和可视化。
网格生成机制
给定一维向量 x(长度 m)和 y(长度 n),meshgrid 输出两个矩阵:
X:每行复制x,共 n 行(y的长度),形状为(n, m)。Y:每列复制y,共 m 列(x的长度),形状为(n, m)。
示例:
import numpy as np
x = [1, 2, 3]; y = [4, 5]
X, Y = np.meshgrid(x, y)
输出:
X = [[1, 2, 3],
[1, 2, 3]] # 每行重复 x
Y = [[4, 4, 4],
[5, 5, 5]] # 每列重复 y
几何意义:网格点坐标为 (X[i,j], Y[i,j]),覆盖所有组合(如 (1,4), (2,4), (3,4), (1,5)...)。
参数解析
1. 索引模式 indexing
'xy'(默认,笛卡尔坐标):输出形状为(n, m),适合绘图(X为横轴,Y为纵轴)。'ij'(矩阵索引):输出形状为(m, n),适合矩阵运算(如线性代数)。
示例:
X_xy, Y_xy = np.meshgrid(x, y) # 形状 (2,3)
X_ij, Y_ij = np.meshgrid(x, y, indexing='ij') # 形状 (3,2)
2. 高维扩展
支持三维网格生成:
x = [1, 2]; y = [3, 4]; z = [5, 6]
X, Y, Z = np.meshgrid(x, y, z) # 输出形状 (2,2,2)
典型应用场景
1. 绘制等高线图(Contour Plot)
import matplotlib.pyplot as plt
x = np.linspace(-3, 3, 100)
y = np.linspace(-3, 3, 100)
X, Y = np.meshgrid(x, y)
Z = np.sin(X**2 + Y**2) # 计算网格点函数值
plt.contourf(X, Y, Z, cmap='viridis')
plt.colorbar()
plt.show()
关键:X, Y 定义网格坐标,Z 为每个点的计算值。
使用其他数组的属性创建相同属性的数组
np.ones_like、np.zeros_like、np.full_like、np.empty_like
创建矩阵数组
np.identity:生成单位矩阵np.eye:生成对角线为1的矩阵,偏移量为可选参数np.eye(5,k = 1) np.eye(5,k = -1)np.diag:创建对角线为任意一维数组的函数,也可指定偏移量(关键字k)
索引和切片
视图
- 使用切片操作从数组中提取的子数组是同一底层数组数据的视图。也就是说,它们引用的是原始数组在内存中的同一份数据,但是具有不同的stides设置。视图中的元素被赋予新值后,原始数组中的值也会随之更新。
- 当需要的是数组的副本而不是视图时,应该使用ndarray的copy方法显式地复制视图
C = B[1:10 1:10].copy()
花式索引fancy indexing
- 可以使用另外一个Numpy数组、Python列表、整数序列进行索引
A = linespace(0,1,11)
A[np.array([0,2,4])] # 取出index为0,2,4的元素
布尔索引
- 索引操作可以很好地和布尔操作结合起来
A[A > 0.5]
- 花式索引和布尔索引得到的不是视图,而是新的独立数组
- 可以使用花式索引和布尔索引来改变所选元素,对其赋值会改变原数组元素的值
调整形状和大小
| 函数/方法 | 说明 |
|---|---|
| np.reshape和np.ndarray.reshape | |
| np.ndarray.flatten | 创建副本,并折叠为一维数组 |
| np.ravel和np.ndarray.ravel | 创建视图,并折叠为一维数组 |
| np.squeeze | 删除长度为1的维度 |
| np.expand_dims和np.newaxis | 增加长度为1的维度 |
| np.transpose,np.ndarray.transpose和np.ndarray.T | 对数组进行转置,即对相应的轴进行反转 |
| np.hstack | 水平叠加,沿着轴1 |
| np.vstack | 垂直叠加,沿着轴0 |
| np.dstack | 深度叠加,沿着轴2 |
| np.concatenate | 沿着给定轴堆叠 |
| np.resize | 根据给定的大小创建原始数组的新副本 |
| np.append | 在数组中添加新元素(会创建新副本) |
| np.insert | |
| np.delete |
使用索引表达式和 np.newaxis 关键字添加新的空轴
data = np.arange(0,5)
column = data[:, np.newaxis]
np.expand_axis(data, axis=1)
row = data[np.newaxis, :]
np.expand_axis[data, axis=0]
数组的拼接和堆叠
- 堆叠函数
data = np.arange(5)
np.vstack(data, data, data)
np.stack()堆叠
一、函数原型与参数
numpy.stack(arrays, axis=0)
arrays:需堆叠的数组序列(列表或元组),所有数组形状必须相同。axis:指定新轴插入位置(默认axis=0)。取值范围为[-ndim-1, ndim],其中ndim是输入数组的维度。
输出形状规律
| 输入形状 | axis 值 | 输出形状 | 堆叠方式 |
|---|---|---|---|
(3,) | 0 | (2, 3) | 整体堆叠(批量维度) |
(3,) | 1 | (3, 2) | 按元素位置堆叠 |
(2, 2) | 0 | (2, 2, 2) | 数组整体作为新维度的切片 |
(2, 2) | 2 | (2, 2, 2) | 同位置元素组成新维度 |
各拼接函数的比较
| 函数 | 维度变化 | 堆叠方式 | 示例输入→输出 |
|---|---|---|---|
np.stack() | +1 维 | 沿新轴堆叠 | (2,2) → (2,2,2)(新增轴) |
np.concatenate() | 不变 | 沿现有轴拼接 | (2,2) + (2,2) → (4,2) |
np.vstack() | 不变 | 垂直堆叠(行方向) | (2,3) + (1,3) → (3,3) |
np.hstack() | 不变 | 水平堆叠(列方向) | (2,2) + (2,3) → (2,5) |
✅ 核心区别:
stack新增维度,而其他函数仅扩展现有维度。
向量化表达式
- 用数组保存数据的目的是希望使用简洁的向量化表达式(vectorized expression)来处理数据,这些表达式能够对数组中的所有元素进行批处理操作。有效地使用向量化表达式能够去除很多显式的for循环
- 二元操作要求表达式中的所有数组都具有兼容大小。
- 兼容大小的含义:表达式中的变量要么是标量,要么是相同形状的数组
形状不同的数组广播的条件
- 当前维度的值相等
- 当前维度的值中有一个是1
Numpy的广播规则:
较小的数组可以通过广播匹配较大的数组。
- 维度不相等,维度较少的数组从左开始填充长度为1的新维度,直到维度一样。
算术运算
- 如果对不兼容大小或形状的数组进行算数运算,则会引发ValueError异常
- 对一两个数组进行算术运算的结果是得到一个新的、在内存中独立存在的数组。
- 使用原位运算(
+=,-=,*=,/=,//=,**=)可以减少内存占用并提高性能。
- 使用原位运算(
逐个元素进行操作的向量化函数
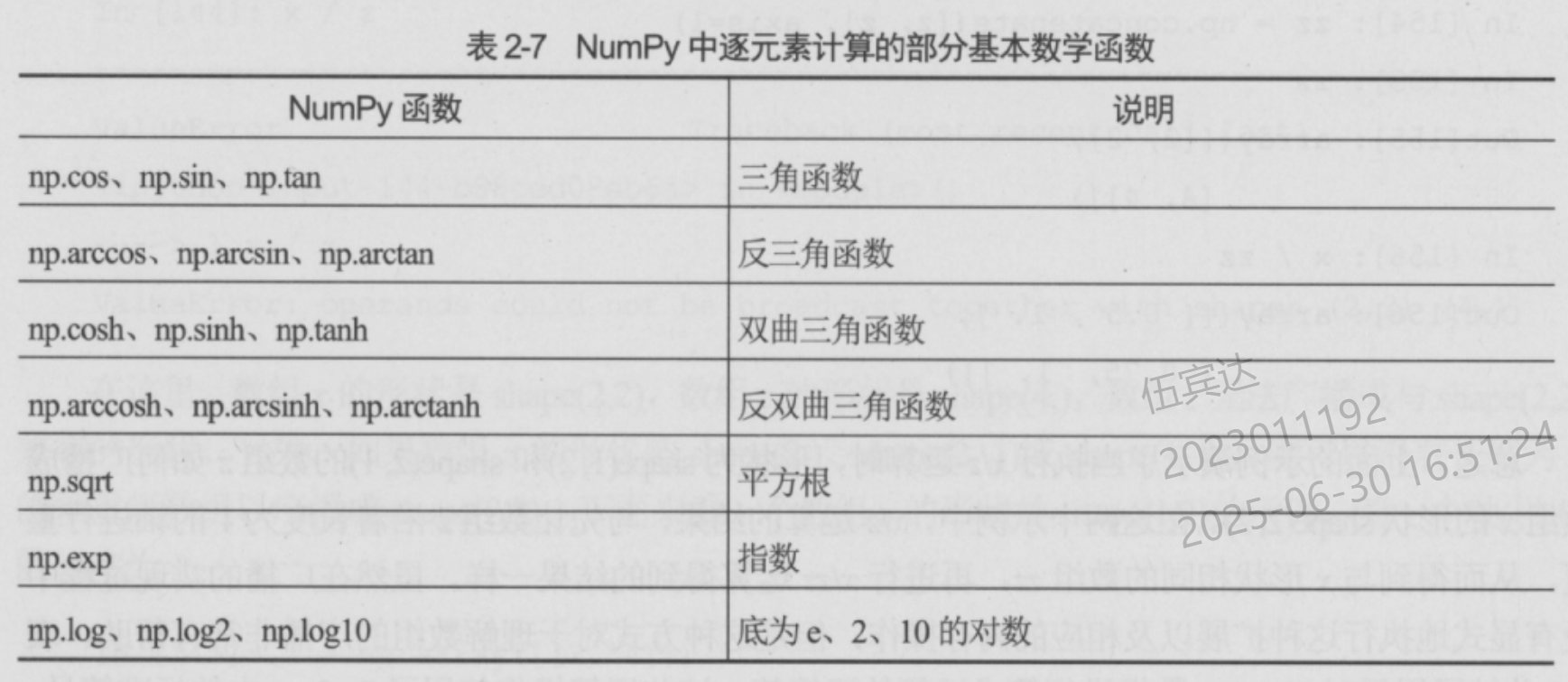
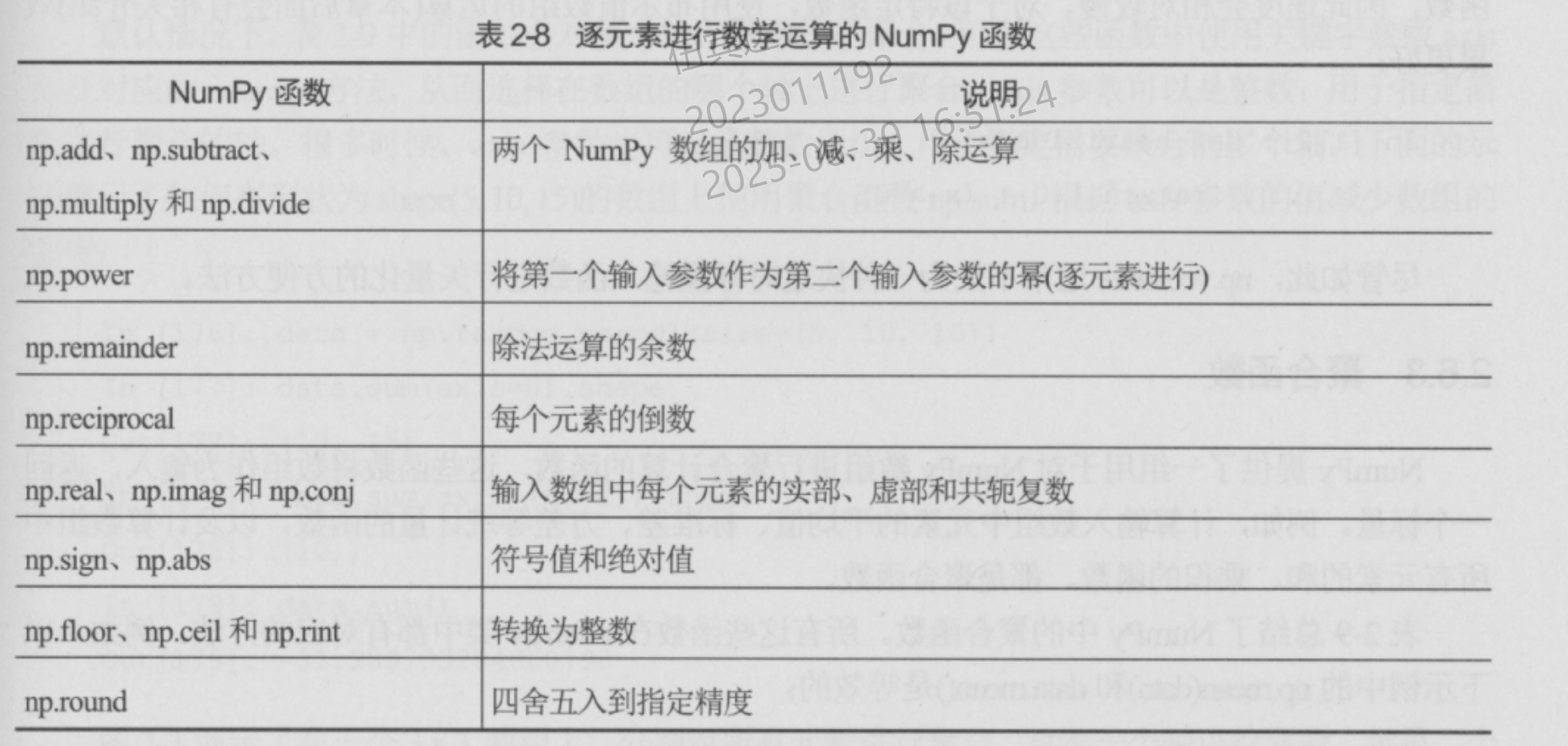
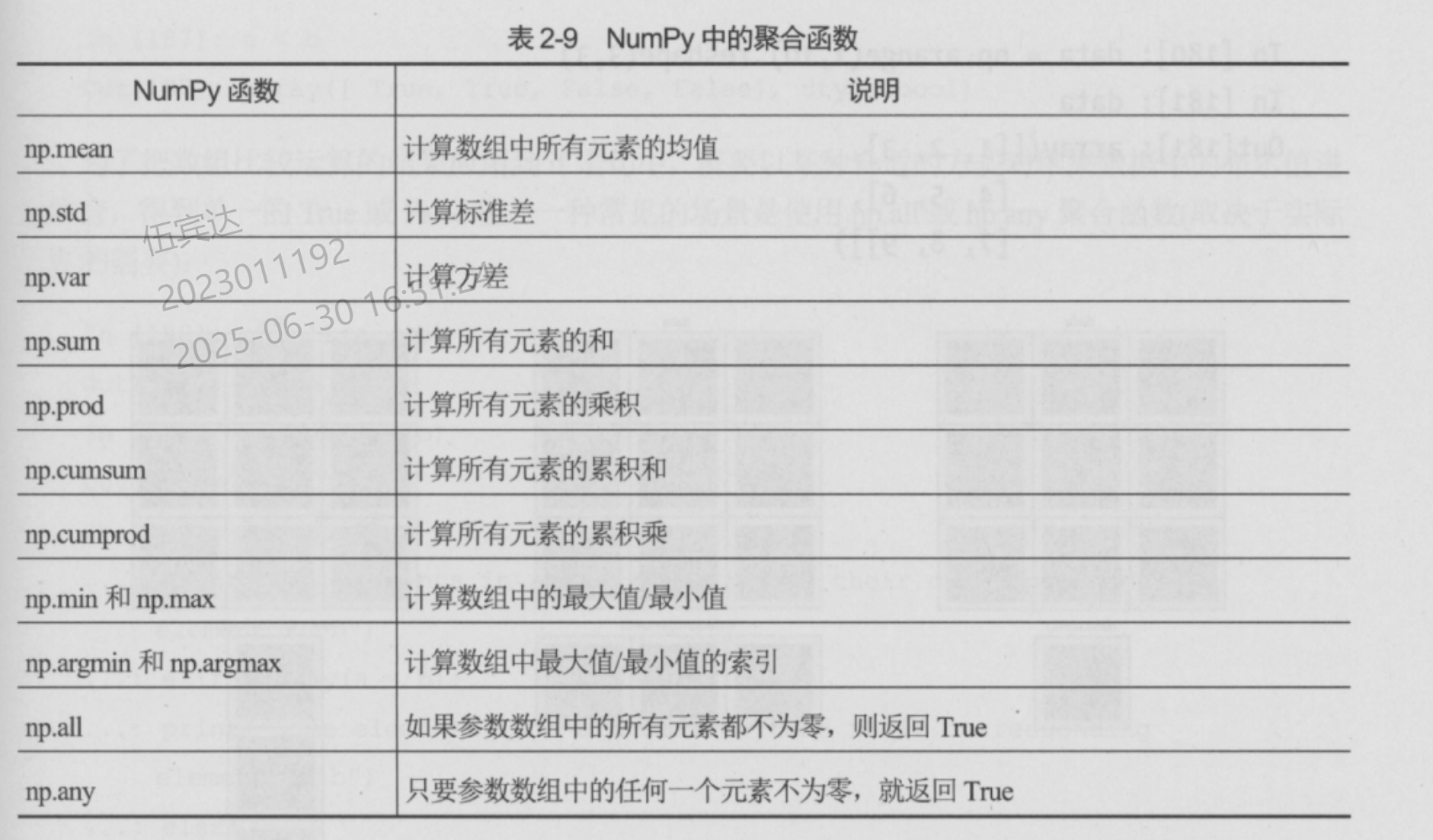
聚合函数
- 数组作为输入,返回一个标量
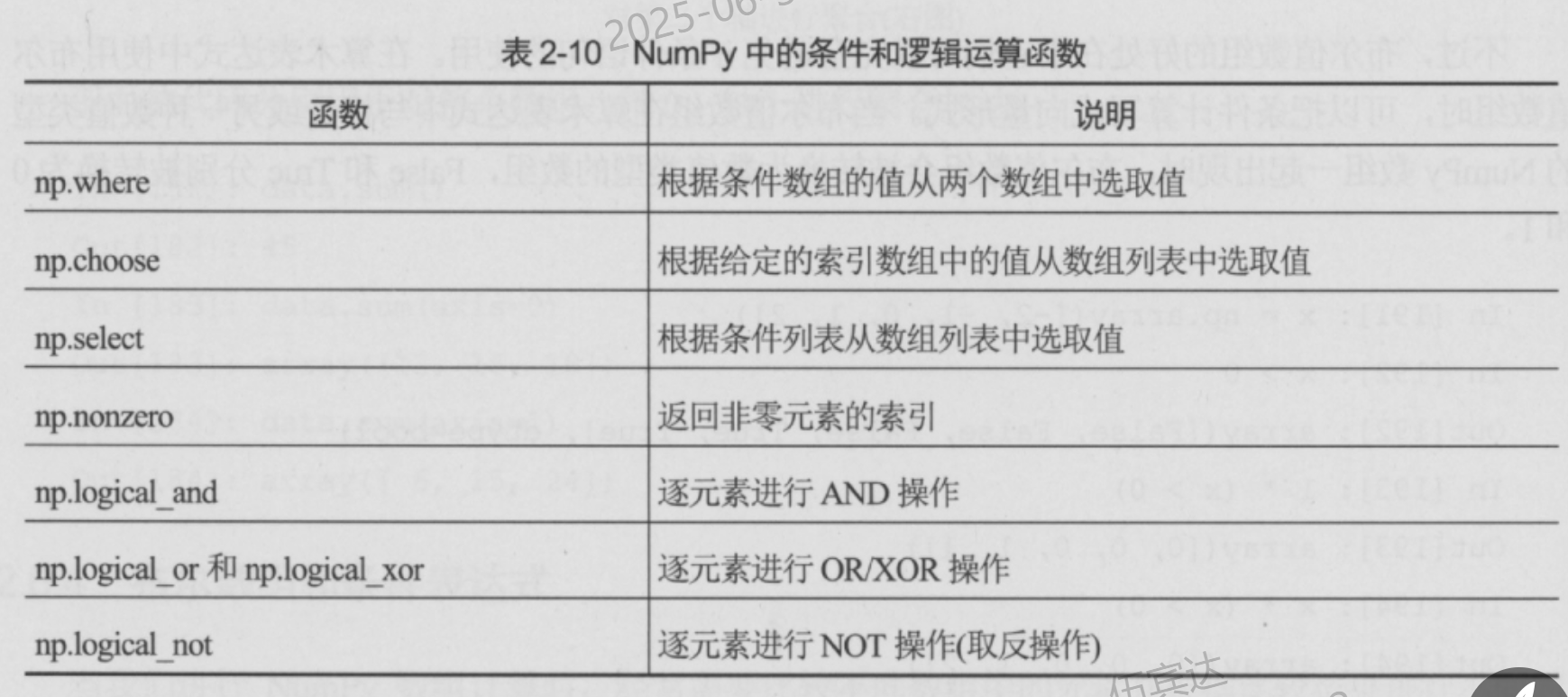
布尔数组和条件表达式
- 广播机制同样适用于比较运算符
- 为了把比较运算的结果应用到if语句中,需要使用np.all和np.any两个聚合函数
- 布尔数组的好处——避免if语句:当布尔值数组在算术表达式中与标量或另一种数值类型的 NumPy 数组一起出现时,布尔值数组会被转换为数值类型的数组,False 和 True 分别被转换为0和1。
A = np.array([-1,-1,0,1,1]) 1*(A > 0) - 这对于条件计算非常有用,例如定义分段函数。如果想要定义描述具有给定高度、宽度和位置的脉冲分段函数,可将高度(标量变量)乘上脉冲的两个布尔值数组来实现:
def pulse(x, position, height, width):
return height * (x >= position) * (x <= (position + width))
集合运算


数组运算

矩阵和向量运算
| 函数 | 说明 |
|---|---|
| np.dot | |
| np.inner | 向量内积(标量积) |
| np.cross | 向量叉积(注意区分outer) |
| np.tensordot | |
| np.outer | 对表示向量的两个数组进行外积(向量的张量积) |
| np.kron | |
| np.einsum |
矩阵乘法
np.dot或者@符号- 一维数组会视情况解释为shape(1,3)或者shape(3,)
外积
若 (\mathbf{u} \in \mathbb{R}^m),(\mathbf{v} \in \mathbb{R}^n),则外积 (\mathbf{u} \otimes \mathbf{v}) 是一个矩阵 (A_{m \times n}),其中 (A_{ij} = u_i v_j)。
示例:(\mathbf{u} = [1, 2]^\top),(\mathbf{v} = [3, 4, 5]^\top),则:
[
\mathbf{u} \otimes \mathbf{v} = \begin{bmatrix} 3 & 4 & 5 \ 6 & 8 & 10 \end{bmatrix}
]
此运算常用于矩阵分解(如SVD)和协方差计算
Kronecker积
又称克罗内克积或直积,它将两个任意大小的矩阵组合成一个更大的分块矩阵。
1. 基本定义
给定矩阵 ( A \in \mathbb{R}^{m \times n} ) 和 ( B \in \mathbb{R}^{p \times q} ),它们的Kronecker积 ( A \otimes B ) 是一个分块矩阵:
[
A \otimes B = \begin{bmatrix}
a_{11}B & a_{12}B & \cdots & a_{1n}B \
a_{21}B & a_{22}B & \cdots & a_{2n}B \
\vdots & \vdots & \ddots & \vdots \
a_{m1}B & a_{m2}B & \cdots & a_{mn}B
\end{bmatrix}{(mp) \times (nq)}
]
其中每个子块 ( a{ij}B ) 是标量 ( a_{ij} ) 与矩阵 ( B ) 的乘积。结果矩阵的维度为 ( (mp) \times (nq) ) 。
2. 计算示例
设 ( A = \begin{bmatrix} 1 & 2 \ 3 & 4 \end{bmatrix} ),( B = \begin{bmatrix} 0 & 5 \ 6 & 7 \end{bmatrix} ),则:
[
A \otimes B = \begin{bmatrix}
1 \cdot B & 2 \cdot B \
3 \cdot B & 4 \cdot B
\end{bmatrix} = \begin{bmatrix}
0 & 5 & 0 & 10 \
6 & 7 & 12 & 14 \
0 & 15 & 0 & 20 \
18 & 21 & 24 & 28
\end{bmatrix}
]
此例中,( A ) 的每个元素被 ( B ) 的完整副本替换并缩放 。
二、核心性质
Kronecker积满足以下代数性质:
| 性质 | 数学表达 | 意义 |
|------------------|-----------------------------------------------------------------------------|--------------------------------------------------------------------------|
| 分配律 | ( A \otimes (B + C) = A \otimes B + A \otimes C ) | 对矩阵加法的兼容性 |
| 结合律 | ( (A \otimes B) \otimes C = A \otimes (B \otimes C) ) | 支持链式运算 |
| 混合乘积 | ( (A \otimes B)(C \otimes D) = (AC) \otimes (BD) ) | 与矩阵乘法的协同性(需维度匹配) |
| 转置 | ( (A \otimes B)^T = A^T \otimes B^T ) | 转置操作的分配性 |
| 逆矩阵 | ( (A \otimes B)^{-1} = A^{-1} \otimes B^{-1} )(若 ( A, B ) 可逆) | 逆运算的独立性 |
| 特征值 | 若 ( \lambda_i ) 是 ( A ) 的特征值,( \mu_j ) 是 ( B ) 的特征值,则 ( \lambda_i \mu_j ) 是 ( A \otimes B ) 的特征值 | 特征值可分解性 |
| 非交换性 | ( A \otimes B \neq B \otimes A )(一般情况) | 运算顺序影响结果 |
三、应用场景
1. 科学计算与工程领域
- 量子计算:描述多量子比特系统的复合状态(如 ( \psi_{\text{total}} = \psi_1 \otimes \psi_2 ))。
- 信号处理:构造多维滤波器,处理多通道信号(如图像、音频)。
- 图论:生成复杂网络的邻接矩阵(如图的笛卡尔积 ( G_1 \times G_2 ) 的邻接矩阵为 ( A_{G_1} \otimes A_{G_2} ))。
2. 数据分析与机器学习
- 协方差建模:构建高维数据的结构化协方差矩阵(如面板数据 ( \Sigma = \Sigma_{\text{时间}} \otimes \Sigma_{\text{变量}} ))。
- 神经网络加速:通过分块计算简化参数矩阵乘法,提升训练效率(如TensorFlow/PyTorch的
kron函数)。 - 图像处理:实现像素级操作(如2倍放大:用 ( \begin{bmatrix} 1 & 1 \ 1 & 1 \end{bmatrix} ) 与图像矩阵做Kronecker积)。
3. 数值优化
- 大规模线性系统:将高维问题分解为低维子问题(如方程 ( AXB = C ) 转化为 ( (B^T \otimes A) \text{vec}(X) = \text{vec}(C) ))。
- 稀疏矩阵表示:高效存储和计算分块稀疏矩阵 。
1. 基础计算工具
- NumPy:
np.kron(A, B)直接计算,适合中小矩阵 。 - PyTorch/TensorFlow:
torch.kron()或tf.linalg.kronecker,支持GPU加速 。
2. 高性能优化策略
| 场景 | 优化方法 | 目的 |
|---|---|---|
| 大矩阵计算 | 分块算法(Blocking) | 减少内存占用 |
| 并行处理 | 多线程/分布式计算(如Spark) | 加速大规模运算 |
| 稀疏矩阵 | 仅存储非零块 | 节省存储空间 |
| JIT编译 | 使用Numba优化循环 | 提升纯Python代码效率 |
代码示例(NumPy):
import numpy as np
A = np.array([[1, 2], [3, 4]])
B = np.array([[0, 5], [6, 7]])
C = np.kron(A, B) # 计算Kronecker积
用kronecker积计算外积
- 要获得与np.outer相同的结果,输入的一维数组必须在np.kron的第一、第二个参数扩展为(N,1),(1,N)
爱因斯坦求和约定
二维数组
identity = np.array([[1, 0], [0, 1]])
print(identity)
[out]:[[1 0]
[0 1]]
二维数组的索引
print(identity[0, 1] is identity[0][1], identity[0, 1] == identity[0][1])
[out]:False True
- 前一种方法是从二维数组中取元素,后一种是先生成一个复制了的一维数组,再取其中的元素,因此 is 判断给出 False ,但它们相等。
square = np.arange(100)
square.shape = (10, 10)
print(square)
- 首先生成了一个长度为 100 的一维数组,随后在保持数据不变的前提下,把它的形状改成了 (10, 10) ,即把它解读成二维方阵。可以理解为数组对象的shape属性是一个tuple,更改了这个属性。
- 这个操作也可以调用 reshape 函数实现:
np.arange(100).reshape((10, 10))
索引取一整行或者列
square[:, 0] # 取出第一列
square[::3, ::5] # 从第一行,列开始每隔3行每隔5列取出元素(Index为3,5倍数的元素,0也匹配)
square[2::3, 3:5] # 从第3(2+1)行开始,每3行取一次
:和::的用法与python的list类似,起始(default值0),终止(default值=维数+1,左闭右开),间隔(default=1)- 当间隔为负数时,例如array[::-1],起始为数组末尾,终止为数组开始。 这很python!!! 符合人类语言。
任意索引(fancy index)
- 分别传两个相等形状的索引数组,按索引数组形状排列对应的输出
print(m6[[1, 2, 3], [3, 4, 5]]) # 给出的新数组的形状由[1,2,3]的形状决定
[out]: [13 24 35]
print(m6[[[1], [2]], [[3], [4]]]) # 输出形状是[[],[]]
[out]:[[13]
[24]]
数组运算
- 可以对numpy数组做各种操作,+-/……以及+=,-=,=,/=等运算符
降维运算
np.mean()函数用于求数组的均值np.std()函数用于求数组的标准差np.var()求方差np.max()函数用于求数组的最大值np.min()函数用于求数组的最小值np.median()函数用于求数组的中位数np.sum()函数用于求数组的和np.prod()函数用于求数组的积
如果只针对某一个维度,使用axis参数指定
np.sum(square, axis=0), np.mean(square, axis=1)
axis=0表示对每一列求和axis=1表示对每一行求均值- 对于多维数组,
axis参数也可以使用tuple,指定多个维度
矩阵的拓展(广播机制)
n[None, :] + n[:, None]
- 使用
n[None, :]得到:[out]:array([[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]])获得一个二维数组,n[:, None]同理 - 对于两个形状不同的数组,
numpy使用广播机制得到:
array([[ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9],
[ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10],
[ 2, 3, 4, 5, 6, 7, 8, 9, 10, 11],
[ 3, 4, 5, 6, 7, 8, 9, 10, 11, 12],
[ 4, 5, 6, 7, 8, 9, 10, 11, 12, 13],
[ 5, 6, 7, 8, 9, 10, 11, 12, 13, 14],
[ 6, 7, 8, 9, 10, 11, 12, 13, 14, 15],
[ 7, 8, 9, 10, 11, 12, 13, 14, 15, 16],
[ 8, 9, 10, 11, 12, 13, 14, 15, 16, 17],
[ 9, 10, 11, 12, 13, 14, 15, 16, 17, 18]])
矩阵运算
元素乘法与矩阵乘法区别
a = b = np.ones((2,2))
print(a * b) # 对应位置元素相乘,输出[[1 1][1 1]]
print(a @ b) # 矩阵乘法,输出[[2 2][2 2]]
张量
- 矩阵可以表示为两个下标的矩阵元:二阶张量
- 三个下标:三阶张量
eps()
- 反对称张量:
eps(n):返回一个n阶反对称张量对应的高阶矩阵(自定义模块asym.py中)
张量乘法
- np.tensordot(),可标注哪些下标进行缩并(内积操作)
a = np.arange(60).reshape((3,4,5))
b = np.arange(24).reshape((4,3,2))
np.tensordot(a,b,axes = ([0,1],[1,0])) # 合并两个方向,输出为一个二阶张量(6-2*2=2)
爱因斯坦约定
eeinsum:a = np.arange(25).reshape(5,5) b = np.arange(5) np.einsum('ii',a) # 取迹 np.einsum('ij->i', a) # 对j方向求和 np.einsum('ij,i', a,b) # 矩阵乘法# 之前的tensordot等价于如下: np.einsum('ijk,jil',a,b) np.einsum('ijk,jil->kl',a,b)- 灵活缩并
a = np.ones(64).reshape(2,4,8) np.einsum('ijk,ilm,njm,nlk',a,a,a,a) #=>4096.0
例:Pauli矩阵
- python中定义的虚数单位
j - numpy中的矩阵乘法运算符
@ - 量子力学中自旋为1/2态空间下的角动量算符表示。
- 这三个矩阵一起,可以看作一个3*2*2的三阶张量
Pauli矩阵的对易关系
pauli = []
pauli.append(np.array([0,1,1,0]).reshape(2,2))
pauli.append(np.array([0,-1j,1j,0]).reshape(2,2))
pauli.append(np.array([1,0,0,-1]).reshape(2,2))
特征值和迹
- NumPy 的 linalg (意为 linear algebra)子模块
np.linalg.eigvals(square) # 计算方阵的特征值 np.trace(square) # 计算方阵的迹 np.linalg.det() # 计算矩阵行列式

- 全反对称张量的含义:
- 全:3*3*3,4*4*4
- 反对称
pauli = np.array(pauli)
(np.einsum('ixy,jxy -> ijxz', pauli,pauli)
- np.einsum('ixy,jxy -> jixz', pauli,pauli)) ==
2j * np.einsum('ijk, kxy', eps(3), pauli) # 或者 np.tensordot(eps(3), pauli, axes = ([2], [0]))
更简单的形式
@符号,重载- 对于矩阵,是矩阵乘法,自动缩并
- 对于张量
# pauli.shape = (3,2,2)
# 对pauli进行拓展:pauli[:,None].shape= (3,1,2,2),pauli[Noen,:].shape = (1,3,2,2)
# 因为之后的两个2*2没有变,所以省略了(pauli[:, None, :, :])
pauli[:, None] - pauli[None, :] # 通过扩展和广播机制,形状变为(3,3,2,2)
# 验证:
np.all(commute(pauli[:, None], pauli[None, :]) ==
2j * np.tensordot(eps(3), pauli, axes = ([2], [0])))

NumPy 中的 np.stack() 函数用于沿新轴堆叠多个同形状数组,生成一个维度更高的新数组。以下是其核心用法详解: